萊迪思半導體公司Ron Warner, Cort Lansenderfer

引言

隨著低成本、低功耗FPGA的出現，加上信號處理應用對性能的要求日益增加，許多傳統用軟件實現的解決方案現在更多地轉移到以硬件為中心的解決方案。如無線通信、軟件無線電技術、醫療圖像和聲納/雷達的應用在很大程度上是依賴于信號處理的，其中所需要的一個主要功能是CORDIC。CORDIC（坐標旋轉數字計算機Coordinate Rotation DIgital Computer）是一種簡化復雜乘法的迭代收斂算法，極大地簡化了整個硬件的復雜性。對于系統設計人員而言，這是一個誘人的選擇，因為根據對下一代信號處理解決方案的提升性能的要求，他們繼續面臨著平衡苛刻的成本和功耗的挑戰。本文綜述了CORDIC算法，以及用可編程邏輯器件來實現的情況。

CORDIC功能的概述

隨著FPGA越來越廣泛地應用于數字通信系統，FPGA支持信號處理的功能也越來越多。對無線世界來說，許多信號處理功能依賴于三角函數，從根本上來說是一系列矢量的旋轉。為了有效地用硬件來實現這些功能，必須找到簡化與其規范形式相關的固有復雜性的方法。CORDIC算法及其擴展算法將矢量旋轉簡化至一系列的移位和加法，大多數FPGA內的結構單元都是支持這兩種算法的。在本節中，我們要討論CORDIC算法，以及如何用它來支持許多與通信系統相關的現代三角函數。

自20世紀50年代以來，CORDIC算法就被人們所知，較初是用于各種數學應用。自那時以來，已在各種基于硬件的器件中實現了該算法，隨著FPGA技術的不斷進步，現在是尋找更好地利用可編程硬件邏輯來求解三角的，線性的和雙曲線功能的時刻。這里關注的重點是CORDIC，它在無線應用中采用了所謂的圓形坐標系統來求解三角函數。如上所述，當用來解決超越函數時，從根本上來說CORDIC是基于矢量旋轉的，如圖1所示。  

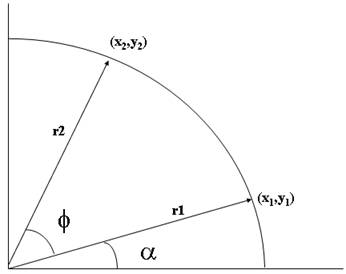
圖1

令r1為原始矢量，我們希望把矢量旋轉到任意的矢量r2的位置(x2,y2)。在單位圓(|r1| = |r2|)上利用一些常見的三角恒等式，我們定義旋轉矢量R1至矢量R2的較終位置為：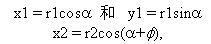

然后運用基本三角恒等式， X2可以表示為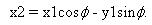

此外對于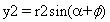

我們可以用類似的替換得到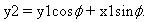

根據通常稱為Givens旋轉的通用矩陣旋轉形式，我們現在可以表達矢量R1和R2之間的關系。

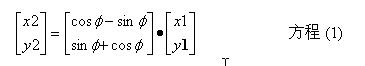
上述方程提供了在二維平面內一種簡單的矢量旋轉方法。對于因子cosf，我們可以重寫方程(1)為，

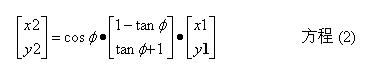
方程(2) 提供了一些矢量旋轉的性質。我們可以看到從R1至R2的矢量旋轉只取決于原來和較終矢量位置之間的夾角，表示為一個標量變量的積，原來矢量的每個分量的和或者差乘以角度的正切，這個角度位于原來的矢量和要求的矢量位置之間。如果我們要進一步定義這個旋轉作為一系列連續的更小微旋轉，比方說q_i取代單個旋轉，我們可以定義旋轉的總和為：

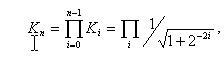
用迭代次數i表示所要求的精度。為了方便硬件上實現，我們定義迭代旋轉角表示為2的冪，即tanf_i = +/-2^-i。此外，旋轉角度可以是正的或者負的; 因此，我們添加了一個變量d_i Î{1, -1} 以記住旋轉的方向。當考慮角度收斂時，使用了變量d。隨著每次迭代，角度收斂，還有一個相關的尺度因子。通過所有的迭代可以定義尺度因子為：

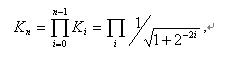
隨著迭代次數的增加，它接近0.6073。圖2提供了CORDIC內增益影響的圖形表示。初始矢量為V0 ，我們希望旋轉到較終的矢量V4。注意通過每一次迭代，總的旋轉角度是如何單調增加的，每次連續迭代的角度相對先前的角度減小了，算法較終收斂于需要的矢量位置。根據精度要求，而不是動態生成尺度因子要求，它可以簡單地存儲在硬件中并與較終的計算結果連系在一起。

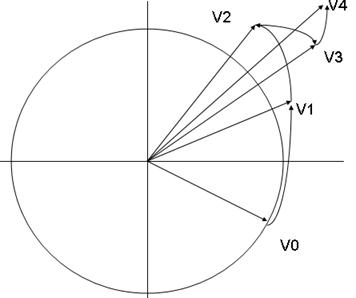
圖2

為了驗證收斂，通過每一次迭代，我們需要記下累積的整個角度，所以需要引進另一個變量，以保持在連續迭代期間累積的整個角度值。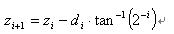

在“ N ”次迭代之后，較終累積的角度可以定義為，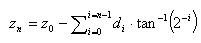

可以看出，z_n含有起始角和累積角之間的差。還應該注意到，角度獨立于“x_i” 和 “y_i”值，只依賴于2^-i 的單調增加值的反正切值。如果每一次連續微旋轉的角度是事先得知的，值可以是硬連線或存儲在FPGA中的某些類型的可讀存儲器中。這樣就減少了角度計算的復雜性，只要跟隨我們的角度累加器進行查找。應當指出的是用更多的旋轉和更小的角度可以達到增加間隔大小，但必須考慮存儲器的要求和性能的權衡。

確保收斂

使用CORDIC收斂有兩個常見的方法：矢量模式和旋轉模式。這兩種方法依賴迭代的次數，并較終限制了可實現的整體性能。因而引入CORDIC算法總是會有一些誤差，因此，只能估計精度，主要是較小位數的位置以及迭代次數。在可編程邏輯器件中實現CORDIC的優點之一是很容易控制這些參數，以滿足所需的精度。

根據上述討論，CORDIC將復雜的功能簡化至一系列移位和加/減的操作，考慮在FPGA內的迭代CORDIC性能時，我們需要考慮硬件架構。在大多數現代的FPGA中，基本邏輯塊整合了直接送入寄存器的邏輯單元。因此，我們可以集中輸入多路復用器的延遲，作為加法器/減法器延時的一部分。可以實現移位器延時，作為內置于FPGA結構中的功能模塊，對加法器/減法器的延時可視為有相同的延時。這是串行實現CORDIC。另外，CORDIC可以利用FPGA所提供的并行性。每一階段的操作和移位邏輯是并行做的，因此，較大的時鐘速度類似迭代法，但總的性能增加了n倍，n是迭代次數。盡管后面設計的邏輯需要n倍邏輯，但總的吞吐量是一個合理的權衡，這取決于較后系統級的要求。作為一個例子，無線基礎設施性能的應用在很大程度上取決于在中頻或基帶頻率實現，以及所選定實現硬件架構的方法（如TDM對比專用的邏輯） 。此外，可編程邏輯器件的靈活性為相應的設計提供了量身定制的功能。

總結

雖然對CORDIC算法有了很好的理解，但用硬件來實現還是較近才發展起來的事。然而，由于設計人員試圖平衡針對新興應用的成本和性能的目標，這很可能會是一個繼續流行的趨勢。正如文中所述，當CORDIC算法是針對低成本FPGA時，對于許多信號處理的應用，它為系統設計人員提供了一個靈活的、節約成本的更高性能的選擇。